16-cell honeycomb
| 16-cell honeycomb | |
|---|---|
Perspective projection: the first layer of adjacent 16-cell facets. |
|
| Type | Regular 4-space honeycomb |
| Family | Alternated hypercube honeycomb |
| Schläfli symbol | {3,3,4,3} |
| Coxeter-Dynkin diagram | |
| 4-face type | {3,3,4} |
| Cell type | {3,3} |
| Face type | {3} |
| Edge figure | cube |
| Vertex figure | 24-cell (Rectified 16-cell) |
| Coxeter group | 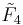 |
| Dual | {3,4,3,3} |
| Properties | vertex-transitive, edge-transitive, face-transitive, cell-transitive |
In four-dimensional Euclidean geometry, the 16-cell honeycomb is the one of three regular space-filling tessellation (or honeycomb) in Euclidean 4-space. The other two are the tesseractic honeycomb and the 24-cell honeycomb. This honeycomb is constructed from 16-cell facets, three around every edge. It has a 24-cell vertex figure.
This vertex arrangement or lattice is called the B4, D4, or F4 lattice.[1][2]
Contents |
Alternate names
- Hexadecachoric tetracomb / Hexadecachoric honeycomb
- Demitesseractic tetracomb / Demitesseractic honeycomb
Coordinates
As a regular honeycomb, {3,3,4,3}, it has no lower dimensional analogues, but as an alternated form (the demitesseractic honeycomb, h{4,3,3,4}) it is related to the alternated cubic honeycomb.
Vertices can be placed at all integer coordinates (i,j,k,l), such that the sum of the coordinates is even.
Kissing number
The vertices of this tessellation are the centers of the 3-spheres in the densest possible packing of equal spheres in 4-space; its kissing number is 24, which is also the highest possible in 4-space.[3]
Symmetry constructions
There are three different symmetry constructions of this tessellation. Each symmetry can be represented by different arrangements of colored 16-cell facets.
| Name | Coxeter group | Schläfli symbol | Coxeter-Dynkin diagram | Vertex figure | Facets/verf |
|---|---|---|---|---|---|
| 16-cell honeycomb | 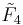 = [3,3,4,3] = [3,3,4,3] |
{3,3,4,3} | 24: 16-cell | ||
| 4-demicube honeycomb | 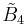 = [31,1,3,4] = [31,1,3,4] |
{31,1,3,4} = h{4,3,3,4} | = | 16+8: 16-cell | |
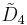 = [31,1,1,1] = [31,1,1,1] |
{31,1,1,1} = h{4,3,31,1} | = | 8+8+8: 16-cell |
See also
- Regular and uniform honeycombs in 4-space:
- k-demicubic honeycombs:
Notes
- ^ http://www2.research.att.com/~njas/lattices/F4.html
- ^ http://www2.research.att.com/~njas/lattices/D4.html
- ^ O. R. Musin (2003). "The problem of the twenty-five spheres". Russ. Math. Surv. 58: 794–795. doi:10.1070/RM2003v058n04ABEH000651.
References
- Coxeter, H.S.M. Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8
- pp. 154–156: Partial truncation or alternation, represented by h prefix: h{4,4} = {4,4}; h{4,3,4} = {31,1,4}, h{4,3,3,4} = {3,3,4,3}, ...
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Richard Klitzing, 4D, Euclidean tesselations x3o3o4o3o - hext - O104